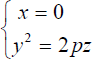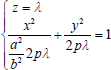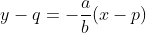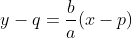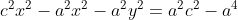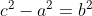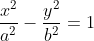PARABOLOIDA ELIPTIK
Pengertian, Rumus, Contoh Soal, dan Jawaban
A. Pengertian Paraboloida
Paraboloida yaitu suatu permukaan yang mempunyai irisan dengan
bidang yang sejajar koordinat tertentu berupa parabola. Jika irisan dengan
bidang koordinat lain berupa elips, maka disebut paraboloida eliptik. Jika
irisan dengan bidang sejajar koordinat yang lain berupa hiperbola, maka
disebut paraboloida hiperbolik.
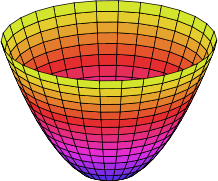
B. Persamaan Paraboloida Eliptik
Paraboloida Eliptik adalah suatu permukaan yang dapat
diletakkan demikian rupa sehingga irisannya yang sejajar bidang
koordinat berbentuk elips dan irisannya yang sejajar bidang koordina
lainnya berbentuk parabola. Berikut ini adalah gambar Paraboloida
Eliptik.
Ellips yang digerakkan terletak pada bidang XOY dengan persamaan
dan garis arah dari ellips yang bergerak adalah parabola pada bidang
YOZ dengan persamaan
=========================================================================
aturan untuk menggerakkan ellips adalah :
a) bidangnya selalu sejajar dengan bidang XOY
b) titik pusat ellips selalu terletak pada sumbu z
c) dua dari puncaknya selalu terletak pada garis arah, dan
d) ellips yang digerakkan selalu tetap sebangun dengan ellips semula.
Misalkan ellips digerakkan sehingga terletak pada bidang z = 𝜆 dan
setengah
sumbu-sumbunya adalah xo dan yo berturut-turut sumbu yang sejajar
sumbu x dan sumbu y.
Karena memenuhi aturan a, b, dan c, maka titik (0, yo, 𝜆 ) terletak pada
ellips , sehingga memenuhi 𝑦0
2 = 2𝑝𝜆
Karena aturan a, b, dan d, maka dipenuhi
atau
Jadi persamaan ellips yang terletak pada bidang z = 𝜆 tersebut adalah :
Persamaan ini merupakan persamaan paraboloida ellips dengan titik
puncak di O. Jika a = b maka persamaan ini menjadi persamaan
paraboloida putaran dengan sumbu z sebagai sumbu putarnya.
Contoh Soal
x = 0, y2 = 16𝑧 dan parabola dengan persamaan digerakkan dengan aturan :
1. Bidangnya selalu sejajar dengan bidang XOY.
2. Titik pusatnya tetap pada sumbu z
3. Dua dari puncaknya selalu terletak pada parabola yang terletak pada bidang YOZ.
4. Ellips tetap sebangun dengan ellips yang digerakkan.
Kita Misalkan ellips pada bidang XOY yang diberikan menjadi :
digerakkan sehingga terletak pada bidang 𝑧 = 𝜆, dan setengah
sumbu-sumbunya adalah x0 dan y0 berturut-turut sumbu yang sejajar sumbu x dan
sumbu y.
Karena memenuhi aturan a, b, dan d, maka titik (0, y0, 𝜆) terletak pada ellips sehingga
memenuhi
Karena aturan a, b, dan d, maka dipenuhi :