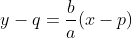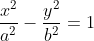Hiperbola
Pengertian, Rumus, contoh soal, dan jawaban
Hiperbola adalah tempat kedudukan titik-titik dalam bidang yang selisih jaraknya terhadap dua titik tertentu adalah tetap(konstan). Selanjutnya dua titik tersebut disebut titik fokus (foci) hiperbola.
- Unsur-unsur hiperbola pada kordinat cartesius
- Sumbu simetri yang melalui kedua fokus disebut sumbu utama (sumbu transvers) atau sumbu mayor dan yang melalui pertengahan F1F2 sedangkan sumbu sekawan (sumbu konjugasi) atau sumbu minor adalah sumbu yang tegak lurus F1F2.
- Titik potong kedua sumbu tersebut disebut pusat hiperbola.
- Titik potong hiperbola dengan sumbu utama disebut dengan puncak hiperbola sedangkan ruas garis penghubung kedua titik potong hiperbola dengan sumbu utama disebut latus rectum.
- Hiperbola mirip dengan parabola, bedanya parabola hanya terdiri dari satu kurva, sedangkan hiperbola terdiri dari dua kurva, yang masing-masing kurva disebut cabang.
A. Hiperbola dengan pusat O(0,0)
Pada hiperbola horizontal
- Titik Puncak atau Koordinat titik puncak adalah perpotongan hiperbola dengan sumbu nyata yakni titik A(a, 0), B( − a, 0) yang jaraknya 2a ( AB=2a).
- Titik Fokus (foci) di
 yang jaraknya 2c
yang jaraknya 2c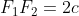
dimana .
. - Titik Pusat adalah titik O yang merupakan titik tengah F1F2.
- Berdasarkan kedudukan titik fokus dan titik puncak diperoleh : AF2 − AF1 = BF1 − BF2 = AF2 − BF2 = BF1 − AF1 = AB = 2a
- Sumbu simetri adalah sumbu x dan sumbu y dengan sumbu utama adalah sumbu x dan sumbu sekawan adalah sumbu y.
- Persamaan garis asimtot dirumuskan
 dan
dan  .
. - Nilai eksentrisitas dinyatakan dengan
 , (e > 1).
, (e > 1). - Panjang Latus Rectum (tali busur yang melalui salah satu fokus dan tegak lurus
sumbu mayor) adalah
 .
.
Pada hiperbola vertikal
- Titik Puncak atau Koordinat titik puncak adalah perpotongan hiperbola dengan sumbu nyata yakni titik A (0, a ), B(0, − a) yang jaraknya 2a.
- Titik Fokus (foci) di
 yang jaraknya 2c
yang jaraknya 2c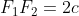
dimana .
. - Titik Pusat adalah titik O yang merupakan titik tengah F1F2.
- Sumbu utama adalah sumbu y dan sumbu sekawan adalah sumbu x.
- Persamaan garis asimtot dirumuskan
 dan
dan  .
. - Nilai eksentrisitas dinyatakan dengan
 , (e > 1).
, (e > 1). - Panjang Latus Rectum (tali busur yang melalui salah satu fokus dan tegak lurus sumbu mayor) adalah
 .
.
B. Hiperbola dengan pusat M(p,q)
Pada hiperbola vertikal
- Titik Puncak atau Koordinat titik puncak adalah di
 .
. - Sumbu utama adalah x = p yang sejajar sumbu y dan sumbu sekawan adalah y = q yang sejajar sumbu x.
- Titik fokus (foci) di
 dan
dan dimana
dimana  .
. - Persamaan garis asimtot dirumuskan dengan
 dan
dan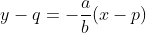 .
. - Nilai eksentrisitas dinyatakan dengan
 , (e > 1).
, (e > 1). - Panjang latus rectum adalah
 .
.
Pada hiperbola horizontal
- Tititk Puncak atau Koordinat titik puncak adalah di

 .
. - Sumbu utama adalah y = q yang sejajar sumbu x dan sumbu sekawan adalah x = p yang sejajar sumbu y.
- Titik fokus (foci) di
 dan
dan dimana
dimana  .
.
C. Persamaan Hiperbola
Persamaan hiperbola dengan titik pusat O(0,0)
Contoh